Historischer Rückblick - Kodierungsvarianten

Das Hauptproblem bei der Kodierung von Textinformationen bestand in der frühen Phase der Computertechnologie darin, dass die verschiedenen Hersteller der Computersysteme, jeweils eigene Kodierungsvarianten entwickelten, die speziell auf die technischen Eigenschaften ihrer Systeme abgestimmt waren.
Die ersten Computersysteme verwendeten bei der Verarbeitung der Daten Zahlenreihen mit einer Länge von 12, 18 oder 36 Bit.
Später verwendeten Computersysteme Wortbreiten von 8 Bit und 16 Bit und verarbeiteten die Daten in Form von "Einheiten" zu je 8 Bit, wobei jeweils 8 Bit als 1 Byte bezeichnet und somit die Daten "byte-weise" verarbeitet wurden.
Eine einzelne Zahlenreihe wird auch als "Datenwort" oder einfach als "Wort" des jeweiligen Computersystems bezeichnet. Die Länge der Zahlenreihe wird dann "Wortlänge" oder auch "Wortbreite" genannt. Auf heutigen Computersystemen sind Wortbreiten von 32 Bit und 64 Bit üblich, bei denen die Daten auch "byte-weise" verarbeitet werden. Daher wird die Speicherkapazität moderner PCs auch immer in Bytes angegeben, z.B. Megabyte oder Gigabyte.
Obwohl immer schnellere und leistungsfähigere Computer entwickelt wurden, die bereits Transistoren und ICs enthielten, wurden lange Zeit auch noch die älteren mechanischen und halbmechanischen Anlagen verwendet, die mit Lochkarten, Relais und Radioröhren arbeiteten.
Das führte dazu, dass Textdokumente, die für Computersysteme kodiert wurden, und die ihre Daten mit einer bestimmten Wortlänge verarbeiteten, nicht auf anderen Computersystemen gelesen oder weiterverarbeitet werden konnten, die ihre Daten mit anderen Wortlängen verarbeiteten.
Aber selbst bei verschiedenen Computersystemen, die ihre Daten mit der gleichen Wortlänge verarbeiteten, wurden unterschiedliche Kodierungsvarianten entwickelt. Diese unterschieden sich zwar nicht durch die Länge der verwendeten Zahlenreihen zur Kodierung der einzelnen Schriftzeichen, wohl aber in der Anordnung der Nullen und Einsen innerhalb der Zahlenreihen.
Ein Textdokument, bei dem z.B. ein "A" mit der Zahlenreihe 1000001 kodiert ist, kann nicht auf einem Computersystem weiterverarbeitet werden, das eine Kodierung verwendet, bei der ein "A" der Zahlenreihe 1110011 entspricht, obwohl ja in beiden Fällen gleichlange Zahlenreihen mit einer Länge von 7 Bit, also jeweils eine 7-Bit-Kodierung verwendet wird.
Um die Austauschbarkeit von Textdokumenten für unterschiedliche Computersysteme zu gewährleisten, mussten sich die Hersteller also auf ein gemeinsames Kodierungsverfahren einigen.
Da die Computer aufgrund der niedrigen Taktraten der damals verwendeten CPUs die Daten nur mit geringer Geschwindigkeit verarbeiten konnten und im Vergleich mit heutigen PCs nur über wenig Hauptspeicher verfügten, bemühte man sich, möglichst kurze Zahlenreihen für die Kodierung zu verwenden.
Die Hauptbestandteile eines Computers sind die Zentraleinheit ("Prozessor"), auch CPU (Central Processing Unit) genannt und der Speicher für die Daten.
- Der Speicher ist in mehrere Speicherzellen unterteilt.
- Jede Speicherzelle besteht aus einer bestimmten Anzahl von Speicherelementen.
- Jedes Speicherelement kann entweder eine Null oder eine Eins speichern.
Ein Computer, dessen Speicherzellen aus jeweils aus 5 Speicherelementen bestehen, kann in jeder Speicherzelle eine Zahlenreihe aus 5 Nullen oder Einsen speichern, also 5 Bit pro Speicherzelle. Speicherzellen, die aus 12 Speicherelementen bestehen, können jeweils eine Zahlenreihe mit einer Länge von 12 Bit speichern.
Bei der Verarbeitung der Daten holt sich der Prozessor die Daten aus dem Speicher. Hierbei wird jedoch nicht der Inhalt eines einzelnen Speicherelements abgerufen, also entweder eine Null oder Eins, sondern immer der gesamte Inhalt einer Speicherzelle, also eine ganze Zahlenreihe, die z.B. eine Länge von 5 Bit oder 12 Bit hat, je nachdem, aus wie vielen Speicherelementen die Speicherzelle besteht.
Diese Zahlenreihe wird in der Computerfachsprache auch als "Datenwort" oder einfach nur als "Wort" bezeichnet.
Mit kurzen Zahlenreihen können jedoch nur wenige Schriftzeichen kodiert werden.
Code-Tabellen
Bei der Zeichenkodierung werden üblicherweise so genannte "Code-Tabellen" erstellt.
Eine Code-Tabelle für eine 5-Bit-Kodierung könnte z.B. so aussehen:

...oder man nimmt statt Zahlenreihen aus Nullen und Einsen, auch "Dualzahlen" genannt, die entsprechenden "Dezimalzahlen"...
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
usw. |
|
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
(jede Dualzahl lässt sich auch als Dezimalzahl schreiben und umgekehrt s. Dualsystem »)
Die Code-Tabelle ist hier aus Platzgründen auf wenige Spalten begrenzt, d.h. sie geht nur bis zum "j".
In Wirklichkeit ist sie jedoch länger und hat 32 Spalten, denn bei einer 5-Bit-Kodierung besteht der Zeichenvorrat aus 32 Schriftzeichen (2 hoch 5 = 32).
Die Menge der zur Verfügung stehenden Schriftzeichen wird auch als "Zeichensatz" (engl.: "charset") oder als "Zeichenvorrat" bezeichnet.
Übersichtlicher ist es deshalb, die Code-Tabelle mit weniger Spalten, dafür aber mit mehr Zeilen zu erstellen:
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0 |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
|
10 |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
|
20 |
u |
v |
w |
x |
y |
z |
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
Wie ließt man nun diese Code-Tabelle ?
- Der Buchstabe "d" steht in der Zeile mit der Bezeichnung "0" und der Spalte mit der Bezeichnung "3". Man rechnet jetzt 0 + 3 = 3. Das Ergebnis lautet also: Der Buchstabe "d" steht in der Code-Tabelle an Position 3.
- Der Buchstabe "r" steht in der Zeile mit der Bezeichnung "10" und der Spalte mit der Bezeichnung "7". Man rechnet jetzt 10 + 7 = 17. Das Ergebnis lautet also: Der Buchstabe "r" steht in der Code-Tabelle an Position 17.
- Die Positionen 26 bis 32 sind in dieser Beispiel-Code-Tabelle noch frei und können z.B. mit Sonderzeichen und Ziffern belegt werden. Der Grund, warum die Position 26 noch frei ist, obwohl das Alphabet ja 26 Buchstaben hat, liegt darin, dass der Buchstabe "a" an Position 0 steht und nicht an Position 1.
- Die Positionen 33 bis 39 liegen außerhalb der Code-Tabelle, die ja nur 32 Positionen hat (hier grau dargestellt).
Code-Erweiterung
Bei einer Zahlenreihe mit einer Länge von fünf Bit lassen sich nur 32 verschiedene Variationen bilden (2 hoch 5 = 32) und somit auch nur 32 Schriftzeichen kodieren, also zuwenig für sämtliche Groß- und Kleinbuchstaben, Sonderzeichen und Ziffern.
Einen Ausweg bot hier das Verfahren der so genannten "Code-Erweiterung" an.
Um mehr Zeichen kodieren zu können, wird eine der noch freien Positionen für das "Umschalten" (engl. "shifting") auf eine so genannte "zweite Ebene" der Code-Tabelle verwendet.
Dazu wird eine zweite Tabelle erstellt, die auch 32 Positionen hat, in der aber andere Schriftzeichen eingetragen werden, die noch fehlen.
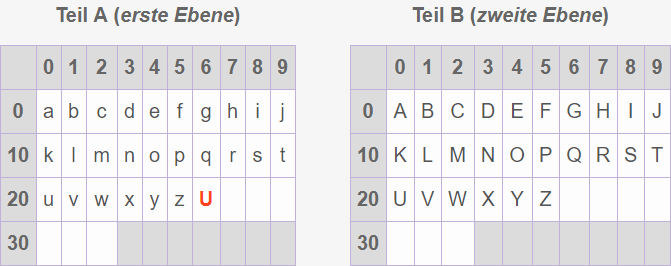
Diese Beispiel-Code-Tabelle hat zwei Ebenen. Wird auf der Tastatur die Taste "m" gedrückt, dann wird die erste Ebene der Code-Tabelle angesprochen und der Code-Wert "12" im Rechner verarbeitet, sodass der kleine Buchstabe "m" auf dem Bildschirm erscheint.
Wird auf der Tastatur die Umschalttaste "U" und die Taste "m" gedrückt, dann wird wieder die erste Ebene der Code-Tabelle angesprochen und zuerst der Code-Wert "26" im Rechner verarbeitet. Das signalisiert dem Rechner, den Code-Wert "12" aus der zweiten Ebene der Code-Tabelle zu nehmen, sodass diesmal der große Buchstabe "M" auf dem Bildschirm erscheint.
Eine andere freie Position könnte dann z.B. für eine weitere Umschalttaste verwendet werden, die auf eine dritte Ebene umschaltet, in der sich an den 32 Positionen statt kleinen oder großen Buchstaben Sonderzeichen und Ziffern befinden. Die hier gezeigten Tabellen wurden so jedoch nie entwickelt und dienen hier nur zur Veranschaulichung, um grundsätzlich zu erklären, wie das Prinzip der "Code-Erweiterung" funktioniert.
Zurückzuführen ist das Prinzip der "Code-Erweiterung" auf den so genannten "Baudot-Code" aus dem Jahre 1870, ursprünglich entwickelt von von Émile Baudot (1845–1903), für ein von ihm entwickeltes Telegrafengerät.
Zeichenkodierung

Da in der frühen Phase der Computertechnologie die ersten Computersysteme in den westlichen Ländern entwickelt wurden, vor allem in den USA, konzentrierten sich die Entwickler von Textverarbeitungsprogrammen zunächst auf die Kodierung von Texten, die auf dem lateinischen Schriftsystem basierten. ...mehr »
Dualsystem (Zweiersystem)

Im Zweiersystem, das auch Dualsystem genannt wird, werden alle Zahlen aus der 0 und der 1 gebildet, also insgesamt aus zwei unterschiedlichen Ziffern... ...mehr »