Zeichenkodierung

Bild: CC0 ↗

Da in der frühen Phase der Computertechnologie die ersten Computersysteme in den westlichen Ländern entwickelt wurden, vor allem in den USA, konzentrierten sich die Entwickler von Textverarbeitungsprogrammen zunächst auf die Kodierung von Texten, die auf dem lateinischen Schriftsystem basierten.

• Eine Schrift besteht aus einer bestimmten Anzahl von Schriftzeichen.
• Diese Anzahl unterscheidet sich stark, je nach verwendetem Schriftsystem

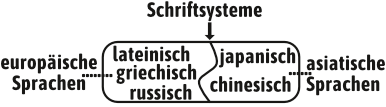
Während Schriftsysteme europäischer Sprachen, wie z.B. lateinisch, griechisch und russisch aus einer relativ geringen Anzahl von Schriftzeichen bestehen, ...

... enthalten die Schriftsysteme asiatischer Sprachen, wie z.B. chinesisch und japanisch eine wesentlich größere Anzahl von Schriftzeichen.

Computersysteme können nur Nullen und Einsen verarbeiten ...

... daher müssen bei der Textverarbeitung auf Computersystemen die Schriftzeichen erst in Nullen und Einsen umgewandelt ("kodiert") werden!

Dies bezeichnet man als "Zeichenkodierung".

Dazu wird jedem Schriftzeichen eine Zahlenreihe aus Nullen und Einsen zugeordnet...

Beispiel:

• die Zahlenreihe 1000001 steht für den großen Buchstaben "A"
• die Zahlenreihe 1100001 steht für den kleinen Buchstaben "a"
• die Zahlenreihe 1000010 steht für den großen Buchstaben "B"
• die Zahlenreihe 1100010 steht für den kleinen Buchstaben "b", usw.

Die einzelnen Nullen und Einsen werden "Bits" genannt...

... die Zahlenreihen in diesem Beispiel haben jeweils eine Länge von sieben Bit.

(Man spricht hier von einer "7-Bit-Kodierung".)

Bei einer Zahlenreihe, deren einzelne Zahlen zwei verschiedene Werte haben können (Null oder Eins) und die eine Länge von sieben Zahlen hat (sieben Bit), lassen sich 128 verschiedene Variationen bilden (2 hoch 7 = 128).

Die folgende Tabelle zeigt alle 128 möglichen Variationen, die sich bei einer Zahlenreihe von nur sieben Bit bilden lassen:

Ist die Zahlenreihe nur ein Bit länger, also acht Bit, sind schon 256 verschiedene Variationen möglich (2 hoch 8 = 256).

Für die englische Sprache reicht die "7-Bit-Kodierung" aus (128 Variationen). Damit lassen sich alle Groß- und Kleinbuchstaben, Sonderzeichen und Ziffern kodieren. Für die japanische Sprache bräuchte man jedoch längere Zahlenreihen.

Historischer Rückblick - Kodierungsvarianten

Das Hauptproblem bei der Kodierung von Textinformationen bestand in der frühen Phase der Computertechnologie darin, dass die verschiedenen Hersteller der Computersysteme, jeweils eigene Kodierungsvarianten entwickelten. ...mehr »

---

GML Verallgemeinernde Auszeichnungssprache

Auszeichnungen, engl. Markups, in einem Text dienten ursprünglich in der Druckindustrie dazu, dem Setzer Anweisungen zu geben, wie der Text in Absätze gegliedert, an welchen Stellen Bilder oder Tabellen... ...mehr »

---